Multiset
From Wikipedia, the free encyclopedia
In mathematics, a multiset (or bag) is a generalization of a set. A member of a multiset can have more than one membership, while each member of a set has only one membership. The term "multiset" was coined by Nicolaas Govert de Bruijn in the 1970s.[1] The use of multisets in mathematics predates the name "multiset" by nearly 90 years; Richard Dedekind used multisets in a paper published in 1888.[2]
The total number of elements in a multiset, including repeated memberships, is the cardinality of the multiset, and the number of times an element belongs to the multiset is the multiplicity of that member. i.e. in the multiset {a, a, b, b, b, c} the multiplicities of the members a, b, and c are respectively 2, 3, and 1, and the cardinality of the multiset is 6.
In multisets, as in sets and in contrast to tuples, the order of elements does not matter. The following list displays the difference between the three concepts, note how a (finite) multiset can also be considered an unordered tuple:
- The tuples (a, b) and (b, a) are not equal, because in tuples order is important; and the tuples (a, a) and (a) are not equal either, because in tuples and multisets multiplicity is considered, affecting cardinality.
- The multisets {a, b} and {b, a} are equal, because in multisets order is unimportant; but the multisets {a, a} and {a} are not equal, as they have different cardinalities.
- The sets {a, b} and {b, a} are equal, like the multisets {a, b} and {b, a}; but the sets {a, a} and {a} are equal, unlike the multisets {a, a} and {a}, this is because in sets, the concept of multiplicity does not exist, or in other words all objects, no matter how many times they belong to the set, still count as one.
Contents[hide] |
[edit] Formal definition
Within set theory, a multiset can be formally defined as a pair (A, m) where A is some set and m : A → N≥1 is a function from A to the set N≥1 = {1, 2, 3, ...} of positive natural numbers. The set A is called the underlying set of elements. For each a in A the multiplicity (that is, number of occurrences) of a is the number m(a). If a universe U in which the elements of A must live is specified, the definition can be simplified to just a multiplicity function mU : U → N from U to the set N = {0, 1, 2, 3, ...} of natural numbers, obtained by extending m to U with values 0 outside A. This extended multiplicity function is the multiplicity function called 1A below. Like any function, the function m may be defined as its graph: the set of ordered pairs { (a, m(a)) : a in A }. With these definitions the multiset written as { a, a, b } is defined as ({ a, b },{ (a, 2), (b, 1) }), and the multiset { a, b } is defined as ({ a, b },{ (a, 1), (b, 1) }).
The concept of a multiset is a generalization of the concept of a set. A multiset corresponds to an ordinary set if the multiplicity of every element is one. However to replace set theory by "multiset theory" so as to have multisets directly into the foundations is not easy: a privileged role would still have to be given to (ordinary) sets when defining maps, as there is no clear notion of maps (functions) between multisets.
An indexed family, ( ai ), where i is in some index-set, may define a multiset, sometimes written { ai }, in which the multiplicity of any element x is the number of indices i such that ai = x. The condition for this to be possible is that no element occurs infinitely many times in the family: even in an infinite multiset, the multiplicities must be finite numbers.
[edit] Multiplicity function
Let us first consider the set indicator function of a normal set, then generalize this concept to the multiplicity function for multisets. The set indicator function of a subset  of a set
of a set 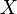 is the function
is the function
defined by
The set indicator function of the intersection of sets is the minimum function of the indicator functions
The set indicator function of the union of sets is the maximum function of the indicator functions
The set indicator function of a subset is smaller than or equal to that of the superset
The set indicator function of a cartesian product is the product of the indicator functions of the cartesian factors
The cardinality of a (finite) set is the sum of the indicator function values
Now generalize the concept of set indicator function by releasing the constraint that the values are 0 and 1 only and allow the values 2, 3, 4 and so on. The resulting function is called a multiplicity function and such a function defines a multiset. The concepts of intersection, union, subset, cartesian product and cardinality of multisets are defined by the above formulas.
The multiplicity function of a join, sometimes called the sum, is the sum of the multiplicity functions
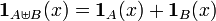 .
.
A small finite multiset, A, is represented by a list where each element, x, occurs as many times as the multiplicity, 1A(x), indicates.
[edit] Examples
One of the simplest and most natural examples is the multiset of prime factors of a number n. Here the underlying set of elements is the set of prime divisors of n. For example the number 120 has the prime factorization
- 120 = 233151
which gives the multiset {2, 2, 2, 3, 5}.
A related example is the multiset of solutions of an algebraic equation. A quadratic equation, for example, has two solutions. However, in some cases they are both the same number. Thus the multiset of solutions of the equation could be { 3, 5 }, or it could be { 4, 4 }. In the latter case it has a solution of multiplicity 2.
[edit] Multiset coefficients
- See also: Stars and bars (probability)
The number of multisets of cardinality k, with elements taken from a finite set of cardinality n, is called the multiset coefficient  (the notation is meant to resemble that of binomial coefficients, and used for instance in (Stanley, 1997); the symbol could be pronounced "n multichoose k" to resemble "n choose k" for
(the notation is meant to resemble that of binomial coefficients, and used for instance in (Stanley, 1997); the symbol could be pronounced "n multichoose k" to resemble "n choose k" for  ). Its value can be given explicitly as
). Its value can be given explicitly as
where the last two expressions express the multiset coefficient in two ways as a binomial coefficient. So, the number of such multisets is the same as the number of subsets of cardinality k in a set of cardinality n + k − 1.
There are for example 4 multisets of cardinality 3 with elements taken from the set {1,2} of cardinality 2, namely : {1,1,1}, {1,1,2}, {1,2,2}, {2,2,2}. And there are also 4 subsets of cardinality 3 in the set {1,2,3,4} of cardinality 4, namely : {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}.
One simple way to prove this involves representing multisets in the following way. First, consider the notation for multisets that would represent { a, a, a, a, a, a, b, b, c, c, c, d, d, d, d, d, d, d } (6 as, 2 bs, 3 cs, 7 ds) in this form:
This is a multiset of cardinality 18 made of elements of a set of cardinality 4. The number of characters including both dots and vertical lines used in this notation is 18 + 4 − 1. The number of vertical lines is 4 − 1. The number of multisets of cardinality 18 is then the number of ways to arrange the 4 − 1 vertical lines among the 18 + 4 − 1 characters, and is thus the number of subsets of cardinality 4 − 1 in a set of cardinality 18 + 4 − 1. Equivalently, it is the number of ways to arrange the 18 dots among the 18 + 4 − 1 characters, which is the number of subsets of cardinality 18 of a set of cardinality 18 + 4 − 1. This is
so that is the value of the multiset coefficient
One may define a generalized binomial coefficient
in which n is not required to be a nonnegative integer, but may be negative or a non-integer, or a non-real complex number. (If k = 0, then the value of this coefficient is 1 because it is the empty product.) Then the number of multisets of cardinality k in a set of cardinality n is
This fact led Gian-Carlo Rota to ask "Why are negative sets multisets?".[citation needed] He considered that question worthy of the attention of philosophers of mathematics.
[edit] Polynomial notation
The set {x} may be represented by the monomial x. The set of subsets, { {}, {x} } , is represented by the binomial 1 + x.
The set {x,y} may be represented by the monomial x·y. The set of subsets, { {}, {x}, {y}, {x,y} } , is represented by the polynomial
- (1 + x)·(1 + y) = 1 + x + y + x·y.
The multiset {x,x} may be represented by the monomial x·x = x2. The multiset of submultisets, { {}, {x}, {x}, {x,x} } , is represented by the polynomial
- (1 + x)2 = 1 + x + x + x·x = 1 + 2·x + x2.
The multiset of submultisets of the multiset xn is
That is why the binomial coefficient counts the number of k-combinations of an n-set.
The multiset xK·yN−K , containing N elements, K of which are hits, is called a statistical population, and a submultiset is called a statistical sample. The set of samples is
- (1 + x)K·(1 + y)N−K
which by the binomial theorem equals
So the number of n-samples with k hits is
See hypergeometric distribution and inferential statistics for further on the distribution of hits.
The infinite set of finite multisets of elements taken from the set {x}:
- { {}, {x}, {x,x}, {x,x,x}, ... }
may be represented by the formal power series
- S = 1 + x + x2 + x3 + ... = 1 + xS .
The formal solution,
- S = (1 − x)−1,
makes sense as a set of multisets, but the intermediate result, 1−x, does not make sense as a set of multisets.
The infinite set of finite multisets of elements taken from the set x·y is
- (1 − x)−1·(1 − y)−1 = 1 + (x + y) + (x2 + x·y + y2) + ...
The special case y=x : The infinite multiset of finite multisets of elements taken from the multiset x2 is
- (1 − x)−2 = 1 + 2·x + 3·x2 + ...
The general case: The infinite multiset of finite multisets of elements taken from the multiset xn is
 .
.
This explains why "multisets are negative sets". The negative binomial coefficients count the number of k-multisets of elements taken from an n-set.
[edit] Cumulant generating function
A non-negative integer, n, can be represented by the monomial xn .
So a finite multiset of non-negative integers, say {2, 2, 2, 3, 5}, can be represented by a polynomial f(x), say f(x) = 3·x2 + x3 + x5 .
It is convenient to consider the cumulant generating function g(t) = log(f(et)), say g(t) = log(3·e2·t + e3·t + e5·t) .
The cardinality of the multiset is eg(0) = f(1), say 3 + 1 + 1 = 5.
The derivative of the g function is g '(t) = f(et)−1·f '(et)·et, say g '(t) = (3·e2·t + e3·t + e5·t)−1 ·(6·e2·t + 3·e3·t + 5·e5·t) .
The mean value of the multiset is μ = g '(0) = f(1)−1·f '(1), say μ = (3+1+1)−1·(6+3+5) = 2.8 .
The second derivative of the g function is g ' '(t) .
The variance of the multiset is σ2 = g ' '(0) .
The numbers ( μ, σ2, ··· ) = ( g '(0), g ' '(0), ··· ) are called cumulants, and that's why g is called the cumulant generating function.
The infinite set of non-negative integers {0, 1, 2, ···} is represented by the formal power series 1 + x + x2 + ··· = (1 − x)−1. The mean value and standard deviation are undefined. Nevertheless it has a cumulant-generating function, g(t) = −log(1−et). The derivative of this cumulant-generating function is g '(t) = (e−t−1)−1.
A finite multiset of real numbers , A = { Ai }, is represented by the cumulant generating function
This representation is unique: different multisets have different cumulant generating functions. See partition function (statistical mechanics) for the case where the numbers in question are the energy levels of a physical system.
The cumulant-generating function of a multiset of n real numbers having mean μ and standard deviation σ is: g(t) = log(n) + μ·t + 2−1·(σ·t)2 + ··· , and the derivative is simply: g '(t) = μ + σ2·t + ···
The cumulant-generating function of set, {k}, consisting of a single real number, k, is g(t) = k·t , and the derivative is the number itself: g '(t) = k . So the concept of the derivative of the cumulant generating function of a multiset of real numbers is a generalization of the concept of a real number.
The cumulant-generating function of a constant multiset, {k, k, k, k, ··· , k} of n elements all equal to the same real number k, is g(t) = log(n)+k·t , and the derivative is the number itself: g '(t) = k , irrespective of n.
The cumulant-generating function of the multiset of sums of elements of two multisets of numbers is the sum of the two cumulant-generating functions:
There is unfortunately no general formula for computing the cumulant generating function of a product
but the special case of a constant times a multiset of numbers is:
The multiset 2·A = {2·Ai} is not the same multiset as 2×A =A+A = {Ai+Aj}. For example, 2·{+1,−1} = {+2,−2} while 2×{+1,−1} = {+1,−1} + {+1,−1} = {+1+1,+1−1,−1+1,−1−1} = {+2,0,0,−2}.
The standard normal distribution is like a limit of big multisets of numbers.
This limit does not make sense as a multiset of numbers, but the derivative of the cumulant generating functions of the multisets in question makes sense, and the limit is well defined.
The constant term k2·log(2) vanishes by differentiation. The terms ··· vanish in the limit. So for the standard normal distribution, having mean 0 and standard deviation 1, the derivative of the cumulant generating function is simply g '(t) = t . For the normal distribution having mean μ and standard deviation σ, the derivative of the cumulant generating function is g '(t) = μ + σ2·t .
See also random variable.
[edit] Free commutative monoids
There is a connection with the free object concept: the free commutative monoid on a set X can be taken to be the set of finite multisets with elements drawn from X, with the obvious addition operation. Such monoids are also known as (finite) formal sums of elements of X with natural coefficents. Compare free abelian group.
[edit] Footnotes
- ^ Knuth, Donald E. (1998). The Art of Computer Programming - Vol. 2: Seminumerical Algorithms, 3rd edition, Addison Wesley, 694. ISBN 0201896842. Knuth also lists other names that were proposed for multisets, such as list, bunch, bag, heap, sample, weighted set, collection, suite.
- ^ Syropoulos, Apostolos (2001), p. 347.
[edit] References
- Blizard, Wayne D. (1989) "Multiset theory," Notre Dame Journal of Formal Logic, Volume 30, Number 1, Winter: pp. 36-66. doi:doi:10.1305/ndjfl/1093634995 http://projecteuclid.org/euclid.ndjfl/1093634995 MR990203 0668.03027
- Bogart, Kenneth P. (2000). Introductory combinatorics, 3rd. ed. San Diego CA: Harcourt.
- Gessel, Ira M., and Richard P. Stanley (1995) "Algebraic enumeration" in Graham, R. L., M. Grötschel, & L. Lovász, eds., Handbook of combinatorics, Vol. 2. Elsevier: 1021-1061. ISBN 0-444-82351-4, 0-444-88002-X, 0-262-07171-1, 0-262-07169-X.
- Multisets are discussed on pp. 1036-1039.
- Hickman, J. L. (1980) "A note on the concept of multiset," Bulletin of the Australian Mathematical Society 22: 211-17.
- Stanley, Richard P. (1997, 1999) Enumerative Combinatorics, Vols. 1 and 2. Cambridge University Press. ISBN 0-521-55309-1, 0-521-56069-1.
- Syropoulos, Apostolos (2001) "Mathematics of Multisets" in C. S. Calude et. al., eds., Multiset processing: Mathematical, computer science, and molecular computing points of view, LNCS 2235. Springer-Verlag: 347-358.














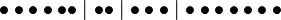

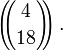




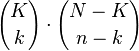




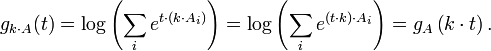
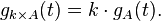








Tidak ada komentar:
Posting Komentar